OPX: Almost, but not quite, what we need to get the Enterprise on the cloud?
A post today by Dana Gardner - Cloud adoption needs a support spectrum of technology, services, best practices - got me thinking again about the importance of a universal "business" identity to make cloud computing a reality for the enterprise sector.
I wrote some time ago about OpenID - the missing spice in Enterprise 2.0? The basic premise being that for Enterprises to truely exploit the exploding cloud offerings, they first need a way of exporting business identities to the web.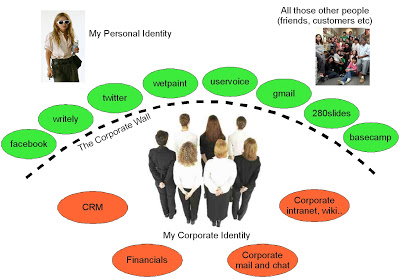
While most businesses at the moment have not officially adopted cloud services, the reality is that cloud services are already penetrating all organisations - whether it is sales people keeping touch with contacts on twitter, pre-sales engineers collaborating via google docs, or consultants using drop.io to get around email size restrictions when sending documents to partners and customers.
The issue I wrote about in my previous post is that we need to wake up and recognise that the flood gates are already open: we are mixing personal and business identities in a tangled mess that is becoming harder to unravel each day.
The risk for business? While free cloud services are giving a tactical boost, when employees move on, they will take all of their cloud-attached contributions with them. At best, a relationship management issue to recover, at worst you find all kinds of SOX and compliance issues lurking to bite back.
Now pretty much all IT-enabled organisations have a form of internal directory and authentication service (be it AD or an LDAP variant). My premise is that organisation do want to be able to exploit google apps, Zoho or Salesforce, but when doing so, we should care deeply that employees apply their business (not personal) identity to any transaction.
From a technologist's point of view, this essentially means that we want to take our internal authentication processes and expose them in a very controlled way on the web. SAML was the deathstar standards approach, but I think in reality OpenID has won the hearts and minds at this point.
One of my projects-on-the-drawingboard is an OpenID provider designed for the Enterprise - a drop in module that allows you to export internal identities from AD or LDAP in a very controlled and auditable way. It is still on the drawing board and has been for ages - if others are interested in making it reality, drop me a line.
However, I think the options may already be available. I am talking about janrain's OPX, although I'm not sure that any of their offerings are really designed for this specific scenario. Even the OPX:Groups offering, which seems to be the closest seems to require establishing a new directory of identities rather than leverging your existing assets. I may be wrong... still investigating and certainly appreciate a steer in the right direction.
read more and comment..
Ubuntu - Linux for Human Beings (and Bears)
Sunshine is one of our pimped PCs. After replacing a totally stuffed hard disk (seriously, it growled like a bear), time to install a real operating system. Sweet!
read more and comment..
Could Open Government initiatives help drive innovation in Singapore?
A few recent stories got me thinking about the status of open data in government, how that translates in Singapore, and in particular the importance of:
- open web publishing standards
- giving priority to open when developing web/data services
First, there was an interesting discussion on open government with Silona Bonewald, founder of the US League of Technical Voters, on the IT Conversations Network. Then the storm-in-a-teacup over a prematurely leaked LTA OPC announcement.
Tim O'Reilly made a convincing summary of the state of play and call for action in his recent O'Reilly Radar presentation at OSCON (and blog post Gov 2.0: It’s All About The Platform). Don't just use our voices to "shake the vending machine"; as technologists we should lend our hands to help prove that open is indeed a better strategy for Government.
And last but not least, Anil Dash posted a great review of the recent initiatives launched by the executive branch of the federal government of the United States in response to President Obama's Open Government Directive. Two notable achievements:
- Whitehouse.gov now publishes exclusively under a Creative Commons Attribution 3.0 License
- data.gov is providing public access to high value, machine readable datasets generated by the Executive Branch of the Federal Government, and I believe is the driver behind some incredibly useful services such as usaspending.gov
The President's CIO Vivek Kundra has since even outlined a vision where the default setting for information created by the government should be public, not secret.
President Obama is racking up some serious credibility for being able to push innovation and adoption in government, and raising the stakes for Governments the world over.
Getting traction in Singapore
As someone who has adopted Singapore as their home, my first reaction was: "it could have been us". It chaffs to see Singapore's world-leading ICT adoption not always translating into world-leading technology innovation and service enhancement.
To be fair, Singapore's iDA Infocomm Adoption Programme and the iGov2010 Strategic Plan encapsulate many of the right sentiments. The issue is timing and rate of change. But for that, Prime Minister Lee Hsien Long could easily have stolen President Obama's thunder.
But I guess the glory of being first isn't the point. Each government must run it's own race, with the focus being on sensible, timely initiatives to improve citizen engagement and stimulate innovation, the economy, and civil society in general.
There are two areas I personally believe deserve priority in Singapore, and are well within reach under the auspices of established strategies:
- Promote citizen engagement by adopting an open publishing standard for Government web sites
- Promote local innovation and technology development by giving priority to "Open" in all Government data initiatives.
Promote citizen engagement by adopting an open publishing standard for Government web sites
Case in point: Did you know that you cannot hyperlink to most government sites without first obtaining explicit permission?
I didn't believe it either until I started checking all the "Terms of Use" statements. This means, for example, that you can't post a link to the MOM list of Public Holidays on your corporate intranet without approval. To say that this flies in the face of how the web is intended to work is putting it mildly (remember what the H in HTML stands for).
mrbrown says it best in relation to the LTA brouhaha:
OPC scheme leaks online before Minister announces it. The internet is here, embargoes don't work. Tough.
Embergoes don't work, neither do attempts to prevent people from linking to a published, public internet website.
While trawling the various government Terms of Use statements, I was also struck by how widely they differ across all the government web properties.
Together, these failures to bring published government websites under some semblance of rational information rights cannot fail to hinder a real engagement of the intended consumers of the information.
Fortunately, the way forwarded has been mapped out clearly: with the example set by Whitehouse.gov, and the brave souls who have laboured over the production of the Singapore adaptation of Creative Commons.
I would dearly love to see the Government adopt a Creative Commons License (perhaps: attribution, no derivative works) as the standard for web site publishing and doing away with all the divergent and restrictive legalese in existing Terms of Use statements.
Why is this important? True citizen engagement and transparency (of the kind attempted by www.reach.gov.sg) will not succeed while Government terms of use still attempt to restrict access and use of information openly published on the web.
The results of my Terms of Use survey? 12 ministries prohibit unauthorised hyperlinking, 4 accept linking (at your own risk). I didn't count stat boards, but they typically have the more restrictive terms.
12 Ministries that prohibit Hyperlinking without Permission - 75% FAIL!
Wording varies, but generally you may only hyperlink to the homepage upon notifying in writing, and for other pages you must make a specific request and secure permission before making a hyperlink. Note that many statutory boards use similar terms. In case you think this may just be a holdover from the internet dark ages, note that all claim to have been "last updated" in the past 3 years, many in 2009.www.gov.sg
www.mcys.gov.sg
www.mewr.gov.sg
www.mfa.gov.sg
www.mha.gov.sg
www.mica.gov.sg
www.mlaw.gov.sg
www.mof.gov.sg
www.moh.gov.sg
www.mom.gov.sg
www.mot.gov.sg
www.pmo.gov.sg4 Ministries that are Hyperlink-friendly - 25% win
The heroes;-)www.mindef.gov.sg
www.mnd.gov.sg
www.moe.gov.sgw
www.mti.gov.sg
Promote local innovation and technology development by giving priority to "Open" in all Government data initiatives
Earlier in August, I saw the latest press release from the Singapore Land Authority and Infocomm Development Authority concerning SG-Space (I would link to SLA's own press release from earlier in the year, but - you guessed it - according to their terms of use, I cannot without prior written permission. Here instead is the non-hyperlinked URL: http://www.sla.gov.sg/htm/new/new2009/new1002.htm)
The goals of SG-Space are laudible - "..to provide an infrastructure, mechanism and policies to allow convenient access to quality geospatial information.." and "..creating a transparent and collaborative environment.." - however it seems to be a good example of how closed, proprietary approaches to innovation still dominate:
- initial rollout will be limited to government agencies, this may mean for years given that this is now a $27m project over 5 years
- the scope seems not only limited to provision of data services, but also includes the provision of applications
- the intent is to extend to the private sector, and to the individual, but the timeframe and commercial basis for this are not clear
The approach has all the hallmarks of the traditional attempt to control and manage innovation through a series of government pilots, before gradually opening up a "fully baked" infrastructure for wider use. Valid, maybe, but one that ignores the lessons from successful API/service innovations such as flickr, google maps and amazon and so on. The open innovation route promises better results, faster:
- going open early drammatically accelerates innovation due to the network effect (a key theme of Patricia Seybold's Outside Innovation
- going open creates the opportunity for unexpected, unplanned innovation (who could have imagined a site like gothere.sg even 5 years ago?).
- by engaging a broader community in the open, much more can be achieved for less (an good example being how gothere.sg allow everyone to contribute missing or new location details)
As Tim O'Reilly put it: DIY on a civic scale (he since adopted a more civic-minded "Do It Ourselves" as suggested by Scott Heiferman)
Although SLA talk about wanting to "Start with pilot projects and be quick to scale up" (Mr Lam Joon Khoi, Chief Executive, SLA), by choosing a closed route there is the distinct possibility that quick just isn't quick enough. Rather than harness the collective energies of the technology community in Singapore, it's more likely to see private efforts stalled completely, or diverted into "Do It Ourselves" initiatives (e.g. OpenStreetMap).
A largely unsung example of how "open" can work very successfully in Singapore is BookJetty. By opening up it's information services, the National Library Board has provided the opportunity for an individual entrepreneur and technologist to combine government and non-government information and create an amazingly compelling service that is not only relevant in Singapore, but also has a global audience.BookJetty is an example of service innovation that the NLB itself could not have attempted. Since the needs that BookJetty serves are at least one step removed from the core mission of the NLB, I doubt they would even be in the position to officially identify and imagine such a service. But by opening their information services to the private sector and individuals, they paved the way for others to innovate in unimagined ways.
Imagine what possibilities there would be for improving the efficiency and level of service if a similar approach was taken to Government Procurement by GeBIZ? http://www.gebiz.gov.sg (sigh, another site that prohibits hyperlinks)
I think it's worthwhile pausing to consider the restrictions imposed by data.gov:
data accessed through Data.gov do not, and should not, include controls over its end use.
This is fundamental to the idea of Government as a Platform. It recognises that government does not have a monopoly on creativity and innovation, and that promoting private sector innovation and entrepreneurship is a priority.
Here is an opportunity for Singapore to greatly boost innovation and ecomomic development by giving early priority to openness in all Government data and service initiatives. The community is certainly brimming with ideas (see what was discussed at a recent WebSG meeting for example).
Singapore seriously does have a small, but vibrant, technology "startup" community. The Government does a great deal to try and stimulate entrepreneurship in this sector, but I would say the results have been middling at best. The main support is in terms of grants and programs (offered by MDA, iDA, Spring and EDB for example), and the opportunity to secure standard government contracts to work directly for the public sector.
Why is this important? I think the time has come to seriously consider how Government can significantly accelerate local technology innovation and economic development by giving serious, strategic priority to opening up it's data and service platform. The iDA Web Services adoption strategy has in fact already lit the path, but it seems to miss the high level push it needs, and a recognition that it most definitely does not mean that Government needs to "Do It All Themselves":
..the programme targets government agencies encouraging them to make available information or services via Web Services. The end result would be citizens making use of richer services via their preferred access points.
Conclusion (or Hypothesis?)
I guess it boils down to a belief that "Open is Better" when applied to government data and services: both for the benefit of civic dialogue and engagement; and to maximise the stimulus for economic development in the local technology sector.
But I wonder if my thoughts are just "outliers"? I'd be very interested to hear more real examples from people of:
- successful innovations that have been enabled through the use of existing open data/services offered by the public sector
- areas you desperately would like to innovate in, but are being held back by closed or inaccessible services
Whether you agree with the priorities I am suggesting or not, I hope most would think that this is an important subject to be discussing.
read more and comment..
Making HackerspaceSG: The Zouk of Geekdom
The technical/geek community in Singapore has been showing some vibrant signs of life in recent times.
-
geekcampsg some 80 or so people gave up their Saturday for 12 solid hours of geekdom - from robotics, to natural language processing, to android development and more -
Singapore Ruby Brigade is going from strength to strength - last Thursday's meetup at wego packed in some 30 people (I guess). They had to kick us out after 10pm and 3 hours of presentations, questions and discussions. That didn't stop most from gathering around the corner for supper that ended after midnight!
The next project is more ambitious: establish a Hackerspace in Singapore. Hackerspaces are community-operated physical places, where people can meet and work on their projects (more)
In order to get this off the ground, a pledge drive has started. Find out how to pledge a donation.
Updated 5-Sep: pledgie no longer being used for the donation drive, so remove the badge
read more and comment..